Trees

Trees types :

• Binary Trees , In a binary tree, k = 2 - Binary Search Trees
• K-ary Trees

Tree components :

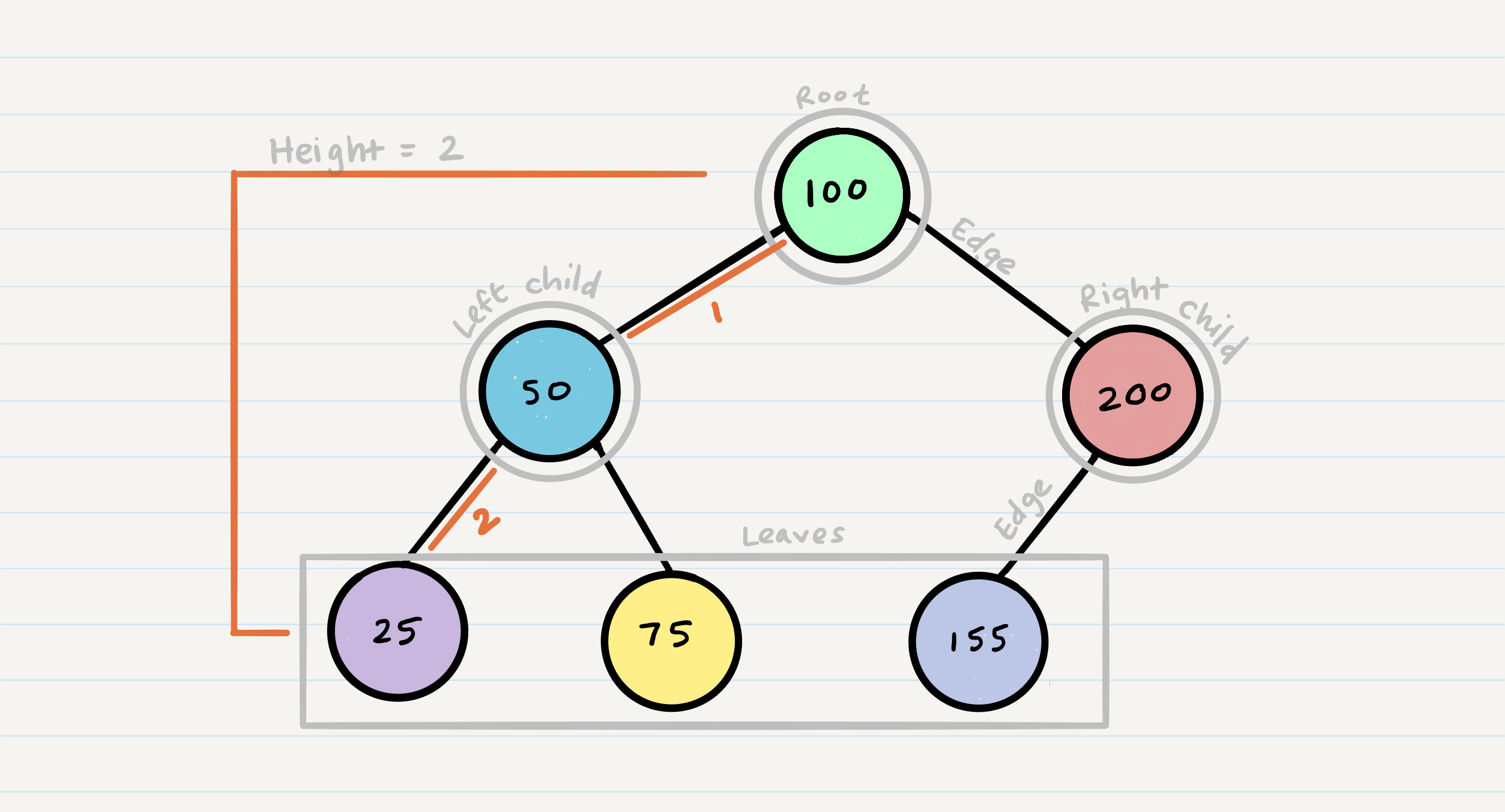
• Node : A Tree node is a component which may contain it’s own values, and references to other nodes (next)
• Root : The root is the node at the beginning of the tree (unique)
• K - A number that specifies the maximum number of children any node may have in a k-ary tree.
• Left : A reference to one child node, in a binary tree
• Right : A reference to the other child node, in a binary tree
• Edge : The edge in a tree is the link between a parent and child node
• Leaf : A leaf is a node that does not have any children
• Height : The height of a tree is the number of edges from the root to the furthest leaf

There are two categories of traversals for trees: Depth First : (use Stack)  There are three methods for depth first traversal: Pre-order: root » left » right In-order: left » root » right Post-order: left » right » root

Breadth First (Use Queue)

The idea of recursion is when we complete a function call, we pop the top node off the stack and are able to continue execution through the previous function call

If root.left and a root.right Both are null, so recursion will end the execution of that method call

Big O The Big O time complexity of a Binary Search Tree’s insertion and search operations is O(h) The Big O space complexity of a BST search is O(1)

The Binary Trees restrict the number of children to two (hence our left and right children) If Nodes of the Tree are able have more than 2 child nodes ,  we call the tree that contains them a K-ary Tree